Mastering GCF and LCM: Fun and Engaging Ways to Teach Kids
Hello, wonderful parents and teachers! Have you ever looked at a math problem involving Greatest Common Factor (GCF) or Least Common Multiple (LCM) and felt like you were staring at ancient hieroglyphics? Fear not! We're here to turn those perplexing problems into a piece of cake with our super fun, easy-to-read, and humor-packed guide on teaching GCF and LCM to kids. Let’s dive in and discover how to make math fun and understandable!
Why Teach GCF and LCM? Before we jump into the methods, let’s talk about why GCF and LCM are important. These concepts are foundational for understanding number theory and are used in various real-world applications, from dividing things into equal parts to finding common denominators in fractions. Plus, they align perfectly with the Common Core State Standards (CCSS), ensuring your students meet key educational benchmarks.
Standards Covered Our GCF and LCM worksheets adhere to the following standards:
- CCSS 4.OA.B.4: Finding factor pairs for numbers 1-100, recognizing multiples, and identifying prime and composite numbers.
- CCSS 6.NS.B.4: Finding the GCF and LCM of whole numbers less than or equal to 100 and 12, respectively, and using the distributive property to express sums.
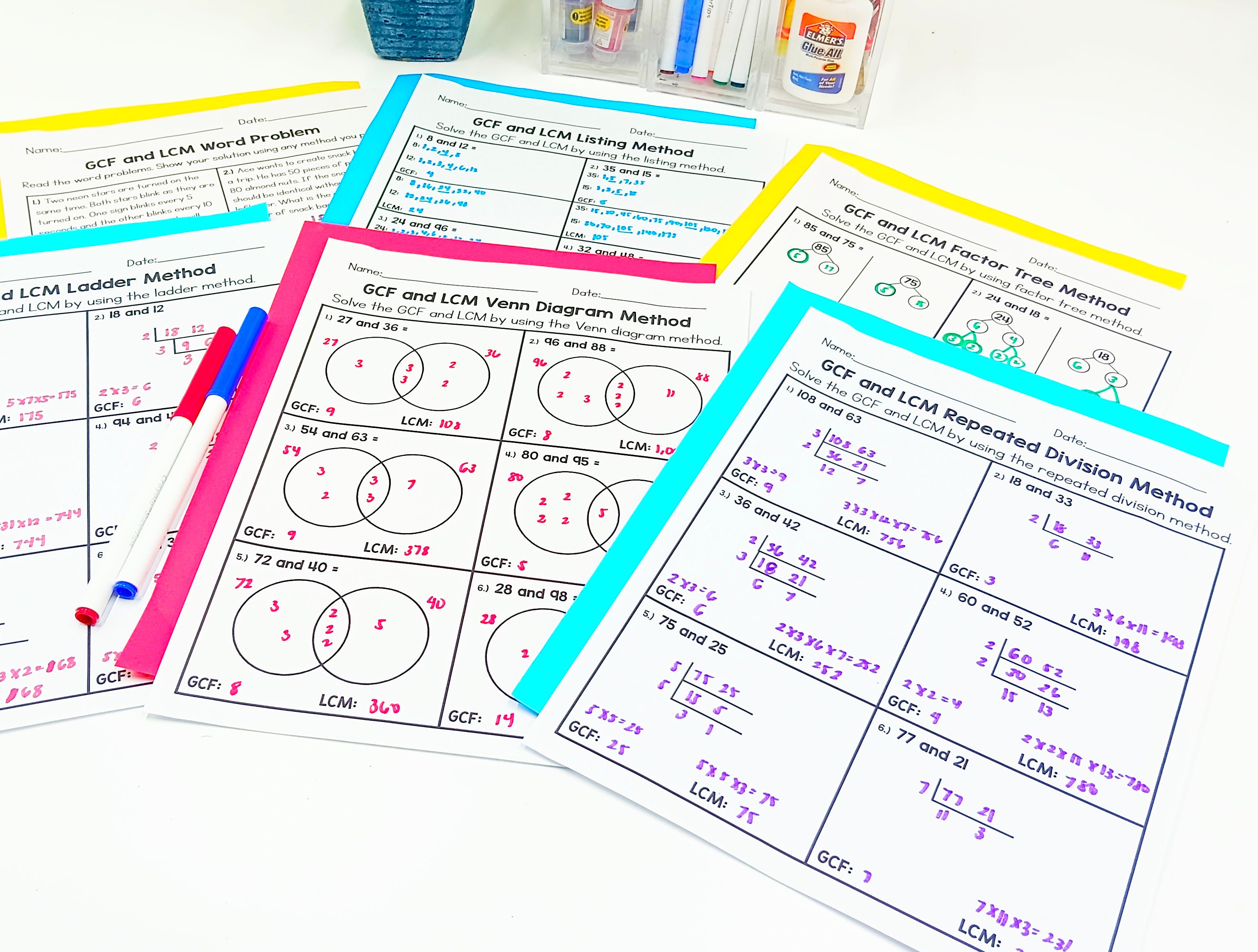
The Fun Methods for Teaching GCF and LCM We’ve got an array of methods to make learning GCF and LCM a breeze. These methods include the ladder method, listing method, factor tree, repeated division, and Venn diagram method. Let’s break each one down with a sprinkle of humor and a dash of simplicity.
1. The Ladder Method
How it works: Picture a ladder. No, not the one you climb to fix that pesky lightbulb. In the ladder method, we use division steps to find the GCF and LCM.
Example:
- Find the GCF and LCM of 24 and 36.
- Start by dividing both numbers by the smallest prime number they share.
- Divide by 2: 24 ÷ 2 = 12 and 36 ÷ 2 = 18.
- Divide by 2 again: 12 ÷ 2 = 6 and 18 ÷ 2 = 9.
- Divide by 3: 6 ÷ 3 = 2 and 9 ÷ 3 = 3.
- Divide by 2: 2 ÷ 2 = 1 and 3 (3 can’t be divided by 2 anymore, so we stop here).
- The GCF is the product of all the divisors: 2 × 2 × 3 = 12.
- The LCM is the product of the GCF and the remaining factors: 12 × 2 × 3 = 72.
Why it’s fun: Kids love the step-by-step process and watching the numbers shrink as they go up the “ladder”.
2. The Listing Method
How it works: List out the multiples or factors and find the common ones. It’s like making a shopping list but less likely to result in ice cream for dinner.
Example:
- Find the GCF of 18 and 24.
- List the factors of 18: 1, 2, 3, 6, 9, 18.
- List the factors of 24: 1, 2, 3, 4, 6, 8, 12, 24.
- The common factors are 1, 2, 3, and 6. The greatest one is 6, so GCF = 6.
- Find the LCM of 4 and 5.
- List the multiples of 4: 4, 8, 12, 16, 20, 24, 28...
- List the multiples of 5: 5, 10, 15, 20, 25, 30...
- The first common multiple is 20, so LCM = 20.
Why it’s fun: Kids can compete to see who can find the common multiples or factors first, turning it into a game.
3. The Factor Tree Method
How it works: Imagine climbing a tree, but instead of finding squirrels, you’re finding prime factors.
Example:
- Find the GCF and LCM of 30 and 45.
- Draw factor trees:
- 30: 30 → 2 × 15 → 2 × 3 × 5
- 45: 45 → 3 × 15 → 3 × 3 × 5
- List the prime factors:
- 30: 2, 3, 5
- 45: 3, 3, 5
- GCF: Multiply the common prime factors: 3 × 5 = 15.
- LCM: Multiply the highest power of each prime factor: 2 × 3^2 × 5 = 90.
- Draw factor trees:
Why it’s fun: Drawing trees appeals to visual learners and adds an element of creativity.
4. The Repeated Division Method
How it works: Keep dividing the numbers by their common factors until you can’t divide anymore. It’s like peeling an onion but without the tears.
Example:
- Find the GCF and LCM of 48 and 60.
- Start dividing by common prime factors:
- 48 and 60 divided by 2: 24, 30.
- 24 and 30 divided by 2: 12, 15.
- 12 and 15 divided by 3: 4, 5.
- The GCF is the product of all the prime factors used: 2 × 2 × 3 = 12.
- The LCM is the product of the GCF and remaining factors: 12 × 4 × 5 = 240.
- Start dividing by common prime factors:
Why it’s fun: It’s satisfying to see the numbers reduce step by step, and it feels like a puzzle.
5. The Venn Diagram Method
How it works: Use Venn diagrams to find the common and unique factors. Think of it as a mathy version of a party Venn diagram showing who likes pizza, ice cream, or both.
Example:
- Find the GCF and LCM of 20 and 30.
- List the factors and place them in the Venn diagram:
- 20: 1, 2, 4, 5, 10, 20
- 30: 1, 2, 3, 5, 6, 10, 15, 30
- Common factors go in the intersection: 1, 2, 5, 10.
- The GCF is the largest common factor: 10.
- The LCM is found by multiplying all unique factors: 2 × 2 × 3 × 5 = 60.
- List the factors and place them in the Venn diagram:
Why it’s fun:
Drawing Venn diagrams is visually engaging and helps kids understand the concept of common and unique factors.
Tips and Tricks for Teaching GCF and LCM
Start with the Basics Begin by explaining what factors and multiples are. Use simple numbers to illustrate the concepts before moving on to GCF and LCM.
Use Real-World Examples Show how GCF and LCM apply in real life, like splitting items evenly or syncing events that occur at different intervals.
Make It Interactive Turn learning into a game. Use flashcards, interactive whiteboards, or online quizzes to keep students engaged.
Reinforce with Repetition Practice makes perfect. Use our worksheets regularly to reinforce concepts and ensure retention. Celebrate Success Praise efforts and celebrate correct answers. Positive reinforcement boosts confidence and encourages learning.
Fun Activities to Teach GCF and LCM at Home and School At Home
- Cooking: Use recipes to show how fractions and multiples work. Divide a recipe in half or double it to find common factors.
- Games: Play number games that involve finding factors or multiples. Card games or board games with a math twist can be very effective.
- Crafts: Use craft supplies to create factor trees or Venn diagrams. It’s a fun way to combine art and math.
At School
- Math Centers: Set up different stations with activities focused on each method. Rotate students through each station.
- Interactive Whiteboards: Use technology to display and solve problems together.
- Group Work: Let students work in pairs or small groups to solve GCF and LCM problems. Collaboration often leads to better understanding.
Real-World Word Problems
Example 1:
Baking Cookies You have 36 chocolate chips and 48 raisins. You want to make cookies with an equal number of each ingredient. What is the maximum number of cookies you can make? Solution: Find the GCF of 36 and 48 using the factor tree method.
- 36: 2 × 2 × 3 × 3
- 48: 2 × 2 × 2 × 2 × 3
- GCF = 2 × 2 × 3 = 12.
- You can make 12 cookies with 3 chocolate chips and 4 raisins each.
Example 2:
Party Planning You’re planning a party and have 12 balloons and 18 party hats. How can you distribute them evenly among the guests?
Solution: Find the LCM of 12 and 18 using the repeated division method.
- Divide by common prime factors: 12 and 18 → 6 and 9 → 2 and 3 → 1 and 1.
- LCM = 2 × 3 × 2 × 3 = 36.
- You’ll need 36 guests to evenly distribute the balloons and hats.
Conclusion Teaching GCF and LCM doesn’t have to be a daunting task. With the right methods, a bit of creativity, and our comprehensive worksheets, you can make learning these concepts fun and engaging for your students or kids. So go ahead, download our worksheets, and let the math fun begin! Happy teaching!
Follow Me for More Teaching Tips with Joy For more tips, resources, and a daily dose of teaching joy, follow me on:
Got questions or want to share your success stories? Drop me an email at thejoyinteaching@gmail.com. I love hearing from fellow educators and parents! Happy Teaching!
Joy Medalla
The Joy in Teaching 💛